Stephen (Sandy) Saperstone's Home Page
Interacting with Ordinary Differential Equations [IODE]
Authors: Stephen Saperstone & Max Saperstone
Access IODE here
[From the AMS website] Interacting with Ordinary Differential Equations is a browser-based interactive digital textbook for the introductory differential equations course. The book takes advantage of the technology in two revolutionary ways. First the expository treatment is layered in a deliberate way. At the highest level the reader can follow the big picture laid out in clear and compelling prose. Upon rereading the reader can follow the imbedded Notelinks that open up to reveal details of calculations and proofs that support the main expository thread. The book also contains scores of Mathematica-based interactive modules. The reader can watch a movie illustrating concepts as they read, or in real time adjust parameters and initial conditions in the models under discussion. The course itself follows a standard modern curriculum with a strong emphasis on visualization. Differential equations are models of motion, now your textbook itself incorporates that motion. This is an exciting and innovative new vision for what a textbook can be in the internet age.
The dynamic feature, which I call interacts, are based on Mathematica notebooks and make this presentation unique. With textual material and interacts for readers to explore solutions and their properties, as well as to investigate the results of changing parameters, both symbolically and graphically, this approach to online content promises to eclipse current offerings in this area. There is no need to load external applications - all interactivity is set within the web page. For instance, a manipulative plot remains embedded in whatever text surrounds it. Motivation, explanation and examples of concepts get first priority; detailed computations and proofs are more secondary. The interacts are built upon the Wolfram Cloud wherein all computations are done.
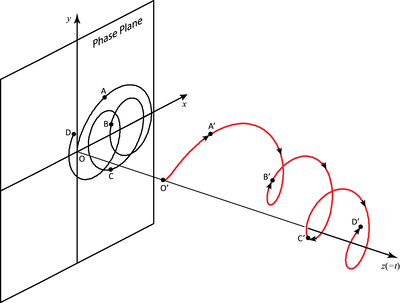
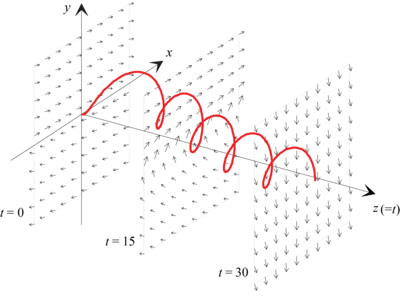
Interacts demonstrate all sort of dynamically controlled “what if’s”, variable slope and direction fields, and parameter dependence of solutions to ODEs. Visualization tools provide a 3D framework for interpretation of implicit solutions to first-order ODEs. Such tools also provide a 3D representation of solutions to 2nd order (or 2D-systems) and their phase plane projections. Applications are interspersed and integrated throughout the Lectures. Examples are drawn from population models, mechanics, biochemical-kinetics, electric circuits, ocean circulation-salinity interactions, and many other areas. The applications not only add a sense of relevance to the study of ODEs, but also provide a common point of experience by which we can analyze and interpret solutions to ODEs. I make a great effort to motivate most topics and to provide interpretations of a geometric or physical nature.
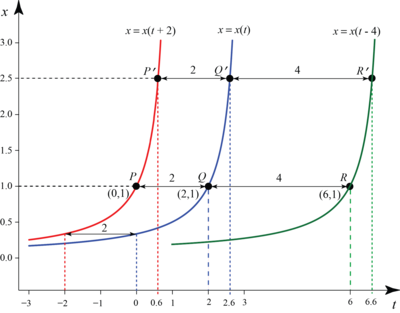
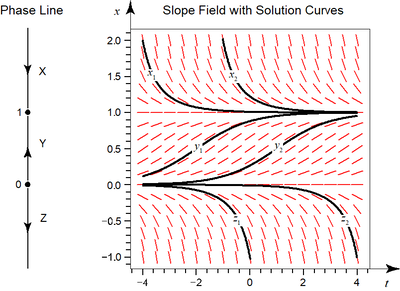
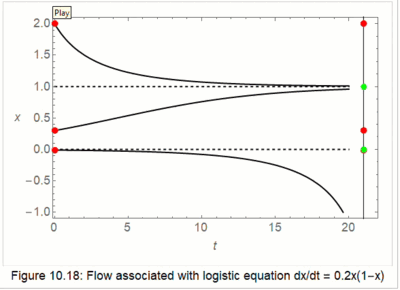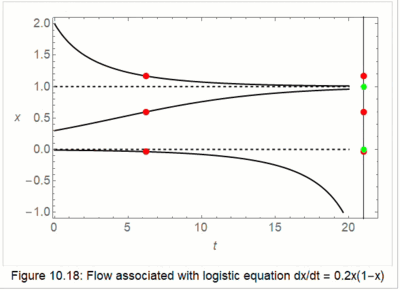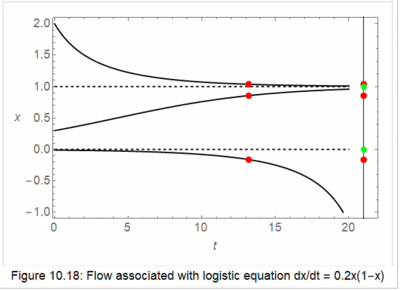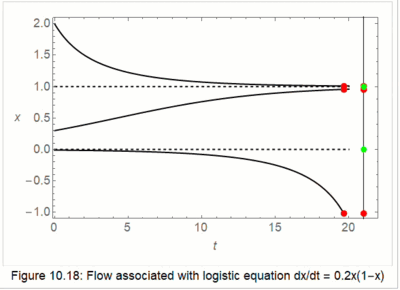
A Gallery of Images from IODE
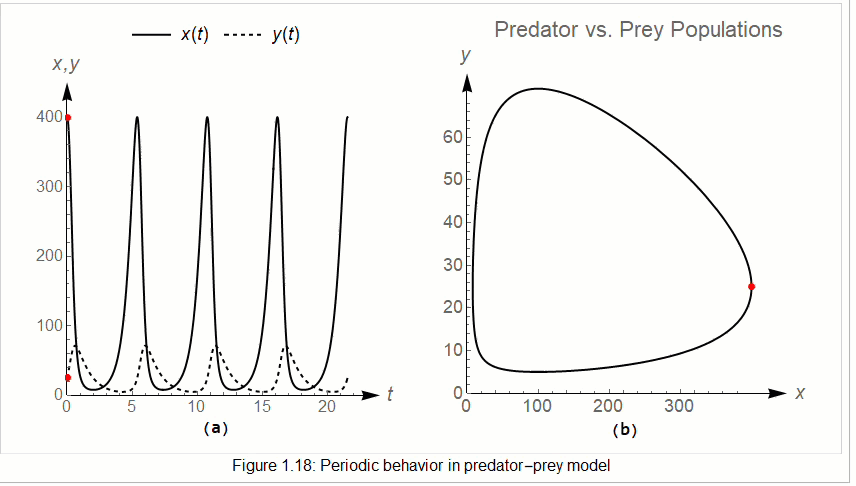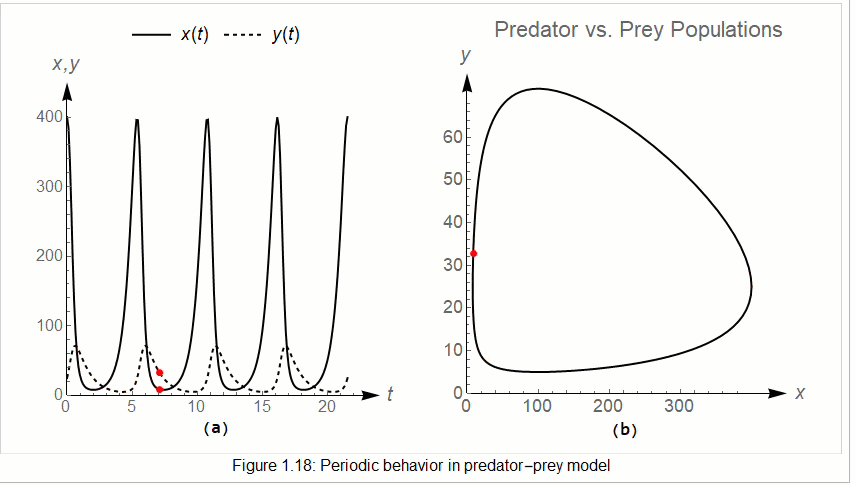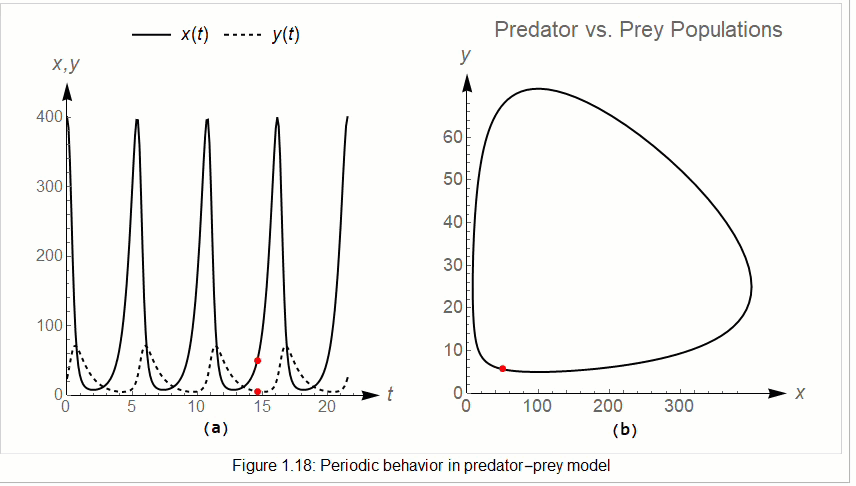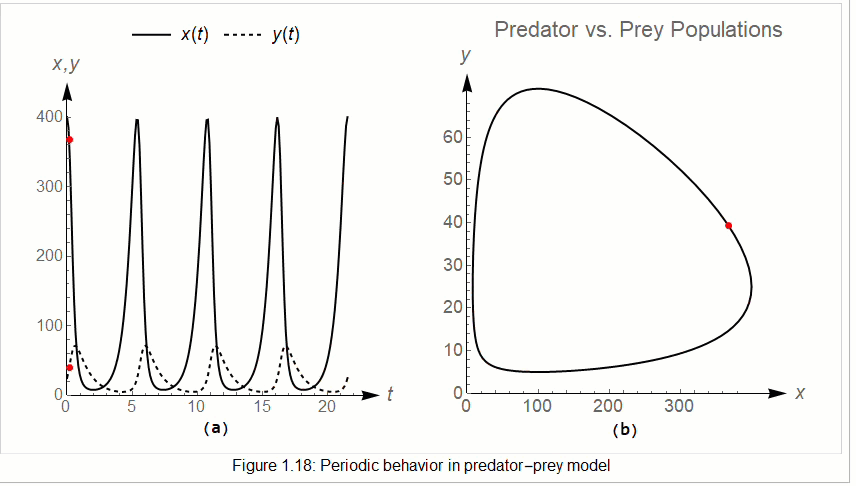
The style of the lectures is based in part on successful teaching strategies that I have used over many years. Typically, I introduce a new topic with a motivating example that demonstrates its need. In other words, I attempt to answer the question, "What is this good for?" Sometimes I provide a "working definition" while properties of the topic are being explored. Another example on the topic is detailed with steps that suggest a generalization. When appropriate, I outline a solution procedure that is followed by yet another example. At this point, if relevant, I introduce formal material. After a concluding example, I provide an explanation, a justification, or even a proof. The nonlinear and interactive features of a web-based treatment of ODEs offer learning opportunities for students heretofore unavailable. I expect that this kind of format will dominate scientific publishing within a few years.
Believe it or not ODEs are not just about "finding" solutions. Indeed, relatively few ODEs have solutions that can be expressed in terms of a formula that you can write down. And we do not "find" solutions as if they were a misplaced document or a lost pair of socks. If we can, we calculate or derive solution formulas; if we can't, we calculate or derive numerical or analytical approximations. Whether we can or cannot solve an ODE, we endeavor to visualize solutions and determine their behavior by other means.
- Graphical and physical models for a better understanding of solution behavior.
- Brief solution procedures for some common ODE forms.
- Routine calculations in many examples, normally “left to the reader,” are found in Notelinks.
- Alerts: Specific areas where students are more inclined to make a mistake are set off by an "ALERT."
- Built-in graphing software to instantly plot explicit or implicitly defined solutions to ODEs.
- Provide geometric explanations for solution behavior.
- Many of the applications are new for a book at this level; e.g., ; ocean circulation-salinity interaction, biochemical-kinetics, a seismometer, and collapse of the Tacoma Narrows Bridge based on aeroelastic flutter.
- A review of linear algebra, complex numbers, and partial fractions.
- A complete hyperlinked index that complements the lectures.